简介
用户一次购买的过程其实包含了许多机器学习的应用,包括物品的展示方式、购物后优惠卷的提供等等。通过查看哪些商品经常在一起被购买,帮助了解用户的购买行为,这种从大规模数据集中寻找物品间的隐含关系被称作关联分析或者关联规则学习。而apriori就是对其思想的算法实现。
有个比较有名的故事:尿布和啤酒。美国的主妇会在丈夫下班时嘱咐他们帮孩子买尿布。店长发现男人们在买尿布的时候还会买啤酒,然后他们就把尿布和啤酒摆在一起。这样做之后大大增加了店里的尿布和啤酒的销量。
这其实就是基于关联规则分析购物篮数据。
问题来了。
如何确定哪些商品经常被用户一次同时购买?
哪写商品一起做促销更能让用户购买呢?
关联分析
频繁项集:在事务数据集合中经常出现一起的物品的集合({牛奶,面包}),生成条件:支持度大于最小支持度
支持度:数据集中包含该项集的记录所占的比例。下图来说,{牛奶,面包}有2条记录包含,所以这个项集的支持度就是2/5。支持度代表项集出现的概率,概率的较低的数据不具备代表性,将被过滤。
最小支持度:支持度的阀值,小于最小支持度的项集不能算是频繁的
关联规则:物品之间存在很强的关系({牛奶}->{面包}表示购买牛奶的人很有可能再购买面包),而关联规则就是我们需要的结果-物品间的强关系,生成条件:规则的置信度大于最小置信度
置信度:是针对关联规则来定义的。拿{牛奶}->{面包}举例子,这条规则代表如果买了牛奶,就有可能还会买面包。在概率论里的意思就是当事件发生X(牛奶)的时候,计算发生Y(面包)的概率,也就是条件概率p(y|x) = p(xy)/p(x),也就是xy同时发生的概率/x发生的概率。用下图举例子就是用户在购买牛奶的时候再次购买面包的概率是:用户同时购买牛奶和面包的概率,除用户仅购买的面包的概率。
最小置信度:置信度的阀值
如果没有支持度,看栗子中的面包和黄油。购买面的时候再次购买黄油的概率为100%,但是并不能说是一条强规则,因为他们本身在一起的发生的概率就很低,所以需要被过滤。如果没有置信度,就不能分辨出一条规则if then的强度。我们需要的是哪些频度高强度高的规则,这样推荐物品用户才能被吸引。
用下面这5个事务集合做解释(1表示购买,0表示未购买)
| transaction ID | 牛奶 | 面包 | 黄油 | 啤酒 | 尿布 |
|---|---|---|---|---|---|
| 1 | 1 | 1 | 0 | 0 | 0 |
| 2 | 0 | 0 | 1 | 0 | 0 |
| 3 | 0 | 0 | 0 | 1 | 1 |
| 4 | 1 | 1 | 1 | 0 | 0 |
| 5 | 1 | 0 | 0 | 1 | 1 |
关联规则的挖掘步骤:
根据事务数据找出所有的频繁项集
依据频繁项集产生强关联规则
Apriori原理
现在有了支持度、置信度,但是该如何高效的找出频繁项集呢?如图所示,这里有{0,1,2,3}4中商品,假如现在我们需要找到{0}的支持度,需要先遍历所有交易的记录,如果记录包含这条项集则count+1,用count/记录总数得到支持度,若大于最小支持度则为频繁项集。
这只是其中的一组数据,图中有个4个商品,若需要全部的频繁项集,需要对项集全部组合方式,有15种,N种商品就会有2的N次方-1种组合方式,商品的增长会造成组合数的急剧上增,而且大多数是无效数据。
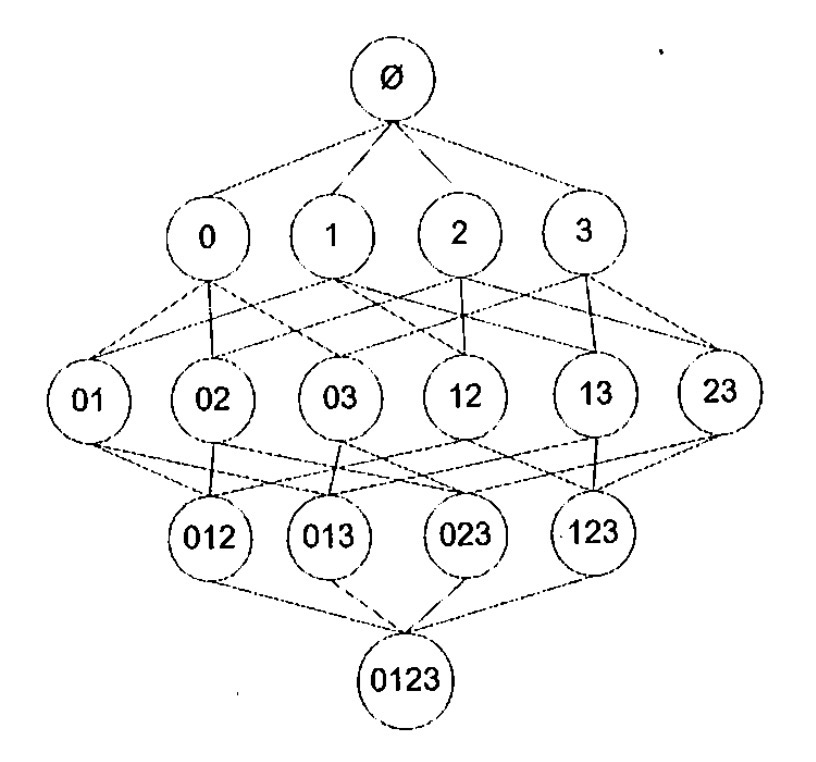
使用apriori减少生成的无效数据
apriori定理:
如果某个项集是频繁的,那么的他的子集也必然是频繁的。
ps:若{0,1,3}的概率大于最小支持度,那么子集{0,3}的概率必然大于最小支持度
相反,如果某个项集是非频繁的,那么他的超集也必然是非频繁的。
ps:若{2,3}的概率小于最小支持度,那么超集{1,2,3}的概率必然小于最小支持度
算法原理:
首先扫描数据集,生成单个物品的项集列表,计算每个项集的支持度,将哪些不满足最小支持度的项集过滤掉。得到一阶频繁项集,再对一阶频繁项集组合生成二阶候选项集,以此类推直到不能再生成项集或者,阶级为项集中物品的数量
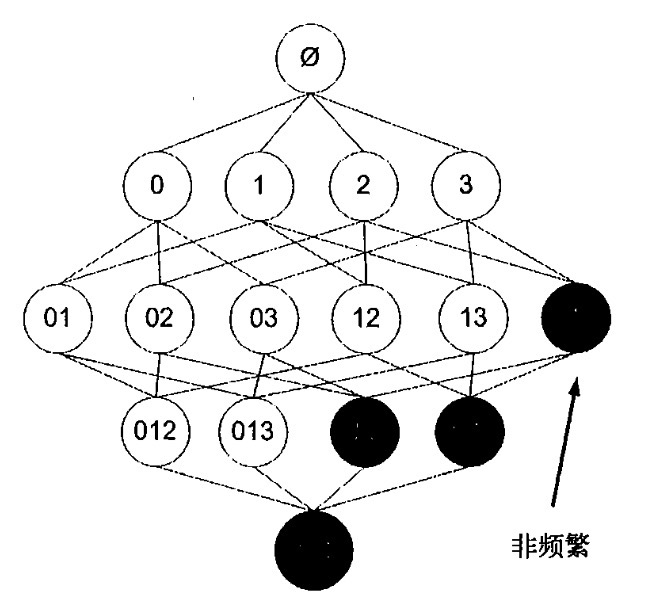
查找频繁项集
扫描所有的记录:
扫描所有的候选项集:
如果候选项集时纪录的子集,增加候选项集的count,表明纪录包含该候选项集的个数
扫描所有的候选项集:
若候选项集的支持度大于最小支持度,则为频繁项集,保留
返回频繁项目集
完整的查找频繁项集:
当前频繁项集不为空
构建一个(k+1阶)组成的候选项集列表 连接
判断每个项集是否频繁的 剪枝
保留(k+1阶)频繁项集
概念不好理解,这里盗个图,如图查找频繁项目集全过程:
计算关联规则
已经得到所有的频繁项集了,如何从一个频繁项目集可以产生关联规则呢,用{0,1,2,3}这个项集来举例,可以得到如下图15种组合方式的关联规则
类似查找频繁项集的原理,如果123->0小于最小置信度,那么该规则的所有子集也会小于最小置信度
123->0 的置信度 = p(0|123) = p(0123)/p(123)
23->01 的置信度 = p(23|01) = p(0123)/p(23)
13->02 的置信度 = p(02|13) = p(0123)/p(13)
12->03 的置信度 = p(03|12) = p(0123)/p(12)
若p(0123)/p(123)小于置信度则p(0123)/p(23)必然小于置信度,因为p(23)>=p(123)
所以根据这个原理减少频繁项集生成无用的关联规则
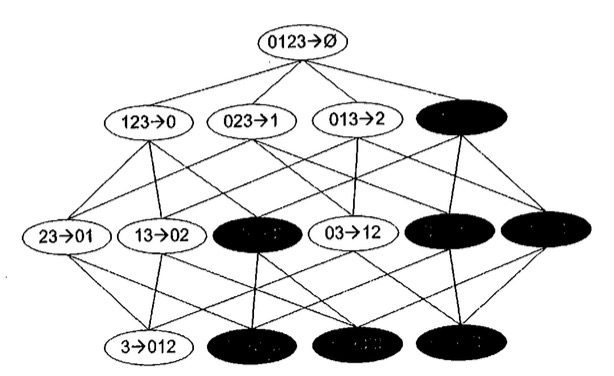
Apriori实现
查找频繁项集
def apriori(dataSet, minSupport=0.5):
largeSet = {} # 总的频繁项集
largeSupport = {} # 总的支持度
c1 = createC1(dataSet) # 创建一阶候选集
l1, supportData = scan(map(set, dataSet), c1, minSupport) # 扫描一阶频繁项集
k = 2 # 下一阶k值
currentLSet = l1 # 当前的频繁项集
while currentLSet:
largeSet[k - 2] = currentLSet # store 当前频繁项集
largeSupport = dict(largeSupport, **supportData) # store 当前支持度到支持度集合中
currentCSet = joinSet(currentLSet, k) # 获得k阶候选集
currentLSet, supportData = scan(dataSet, currentCSet, minSupport) # 扫描k阶候选集,得到频繁项集
k += 1
return largeSet, largeSupport
计算关联规则
def rules(largeSet,largeSupport,minConf = 0.5):
rules = []
for key,value in largeSet.items()[1:]: #从二阶频繁项集集合开始计算
for item in value : #遍历k阶的频繁项集
subsets = map(frozenset,subset(item)) #计算某个频繁项集的所有子项集
for element in subsets : #遍历所有子项集
remain = item.difference(element) #计算后置项
if(len(remain) > 0): #有后置项
confidence = largeSupport.get(item)/largeSupport.get(element) #计算关联关系置信度
if confidence > minConf:
rules.append((tuple(element),tuple(remain),confidence))
return rules
完整代码
https://github.com/whx4J8/machine-learn.git
